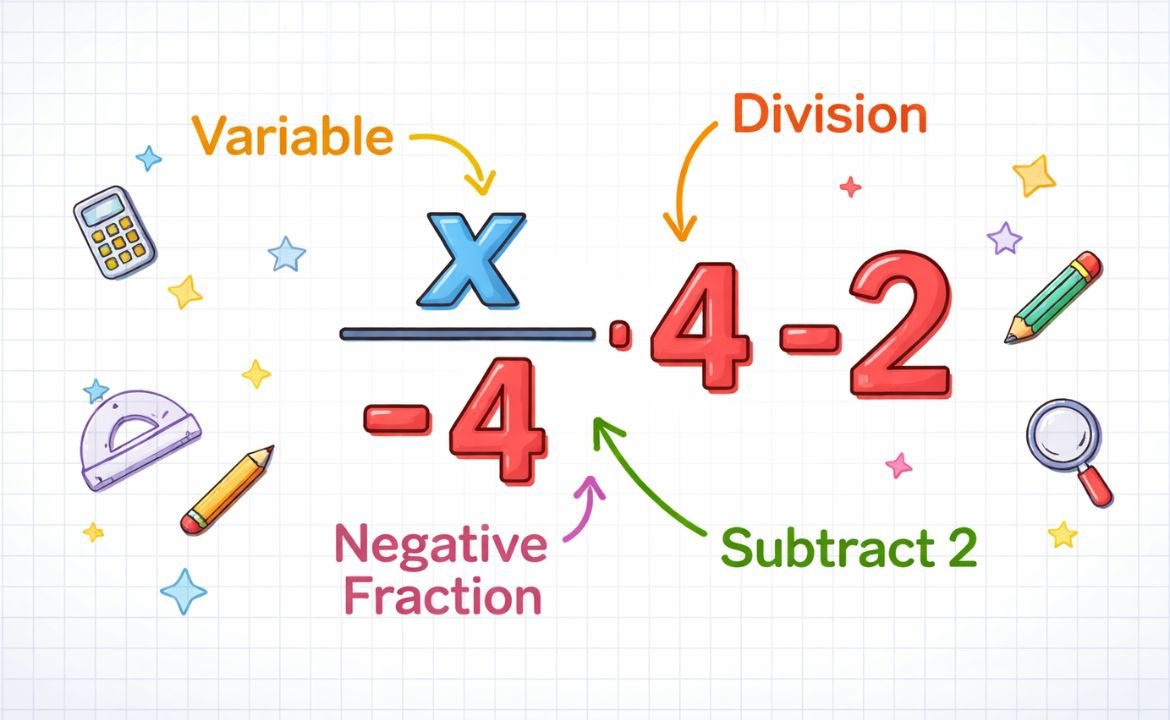
The expression x/-4 -2 looks simple, yet it represents several important algebraic ideas. At its core, it combines division, variables, and subtraction into a compact mathematical form. Learning how to read and manipulate expressions like this builds a strong foundation for algebra, problem solving, and logical reasoning. Many students encounter similar structures when simplifying equations, solving for unknown values, or analyzing linear relationships. By breaking the expression into parts, anyone can understand what it communicates and how to work with it confidently.
Algebra is essentially a language that describes patterns. In this case, the expression x/-4 -2 shows how the variable x represents an unknown value. Dividing that value by negative four introduces scaling and sign changes. Subtracting two then shifts the result. These operations together model transformations that appear in real-world calculations, from budgeting to physics formulas. Understanding each step prevents confusion and helps learners see algebra as a structured system rather than a collection of rules.
Expressions that mix division and subtraction often highlight order of operations. Division occurs before subtraction, ensuring consistency in interpretation. When students internalize this structure, they gain accuracy and speed. They also become better at spotting equivalent forms, such as rewriting division as multiplication by a fraction. This flexibility is crucial in higher mathematics, where expressions grow more complex but rely on the same core principles.
Breaking Down the Structure of the Expression
To understand the mechanics, start with the division component. The term x/-4 means the variable is scaled by a negative fraction. This operation flips the sign and reduces magnitude. Conceptually, it is the same as multiplying x by negative one quarter. Seeing this equivalence makes simplification easier and supports mental math skills.
Next comes the subtraction of two. This constant shifts the value downward on a number line. When graphing the expression as part of a function, this subtraction represents a vertical translation. Recognizing these visual interpretations helps learners connect symbolic math with graphical meaning.
Interpreting Signs and Direction
Negative signs often intimidate beginners, yet they follow consistent logic. Dividing by a negative produces an opposite direction. When combined with subtraction, the final result depends on the value of x. Practicing sign rules improves confidence and reduces calculation errors. Over time, these operations feel intuitive rather than mechanical.
Simplification and Equivalent Forms
Mathematical fluency grows when students learn to rewrite expressions in multiple ways. The expression can be expressed as:
−x4−2-\frac{x}{4} – 2−4x−2
This format emphasizes multiplication by a fraction instead of division. Many algebraic manipulations become clearer in fractional form. For example, combining like terms or solving equations often benefits from consistent notation.
Simplifying does not change meaning. Instead, it reveals structure. When learners recognize patterns, they can apply algebraic properties such as distribution or factoring more effectively. These skills extend to equation solving, where isolating variables is essential.
Practical Simplification Strategies
A helpful approach is to separate operations. First handle division or fractional multiplication. Then apply subtraction. Writing each step clearly reduces mistakes. Checking results by substitution reinforces understanding and builds trust in the process.
Applications in Real-World Problem Solving
Expressions similar to this appear in financial modeling, measurement adjustments, and rate calculations. Imagine distributing a quantity evenly while accounting for a fixed deduction. The structure mirrors division followed by subtraction. Recognizing this pattern allows faster translation from words to equations.
In physics or engineering contexts, scaling and offsetting values are common. A sensor reading might require calibration using a formula with division and subtraction. Understanding algebraic expressions ensures accurate interpretation of such formulas.
Building Analytical Thinking
Working with algebra trains logical reasoning. Each operation has a purpose and predictable effect. By analyzing expressions step by step, learners strengthen problem-solving habits that transfer beyond mathematics. This structured thinking supports coding, data analysis, and scientific inquiry.
Common Mistakes and How to Avoid Them
One frequent error is misapplying order of operations. Some learners subtract before dividing, which changes the result. Remember that division or multiplication comes first. Writing parentheses during practice can clarify intended order.
Another mistake involves sign confusion. Losing track of negative values leads to incorrect answers. Slow, deliberate steps help maintain accuracy. Verifying work with sample numbers is a reliable safety check.
Strengthening Algebra Confidence
Confidence grows through repetition and reflection. Practice rewriting expressions, evaluating them with different values, and explaining each step aloud. Teaching a concept to someone else is a powerful reinforcement method. Over time, the logic behind algebra becomes second nature.
Why Mastering Expressions Matters
Algebraic expressions are building blocks for equations, functions, and advanced mathematics. Understanding how division and subtraction interact prepares learners for linear equations and graph analysis. These skills support academic success and practical reasoning.
Mathematics is less about memorizing formulas and more about recognizing relationships. When students see how variables transform under operations, they gain insight into broader mathematical systems. This awareness fosters adaptability and curiosity.
Long-Term Learning Benefits
Strong algebra foundations improve performance in science, technology, and economics. The habits developed while analyzing expressions encourage precision and persistence. These qualities are valuable in any analytical field.
Conclusion
The expression x/-4 -2 is more than a simple algebraic statement. It demonstrates scaling, sign behavior, and value shifting in a compact form. By breaking it down, rewriting it, and practicing interpretation, learners gain clarity and confidence. Mastering expressions like this strengthens mathematical thinking and prepares students for more advanced challenges. With consistent practice and attention to structure, algebra becomes a logical and empowering tool rather than an obstacle.